初识haystack
去年就关注到了haystack这个框架,那会儿还不是很完善。今年再次看到haystack发现已经很完善了。
在17年的时候曾经基于RASA框架写过一篇关于如何打造一个chatbot的文章,很粗浅的介绍并写了一个chatbot。QA在NLP领域一直受到很多的关注,比如AIML就是早期的用于开发chatbot的标记语言。随着深度学习时代的到来,各项NLP技术日新月异、百花齐放,业界对NLP技术本身的关注远大于QA的关注。16年的RASA框架提供了将NLP技术应用于QA的一种解决方案,但这种方案耦合性依然很高,尤其是对话管理部分,对比下来自己研发一个框架还来得容易些。
haystack的特点
Haystack框架的主要贡献在于:
- 1.集成当前最新的NLP技术,比如transitformer,SQuAD;
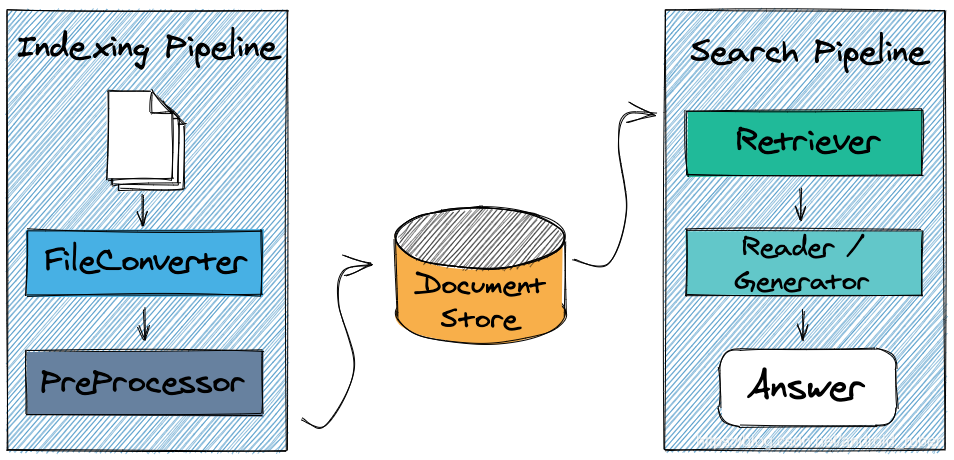
- 2.完全端到端,开箱即用,提供Converter、Retriever、Reader、Generator等组件;
- 3.集成了es、sparql等数据库;
- 4.集成标注工具。
graph LR
预处理语料-->存储语料-->构造QA模块-->答案
按照这个设计,haystack的实现也非常的简单:
1
2
3
4
5
6
7
8
9
10
11
#预处理
dicts = convert_files_to_dicts(dir_path=doc_dir, clean_func=clean_wiki_text, split_paragraphs=True)
#存储语料
document_store = ElasticsearchDocumentStore(host="localhost", username="", password="", index="document")
document_store.write_documents(dicts)
#构造QA模块
retriever = ElasticsearchRetriever(document_store=document_store)
reader = FARMReader(model_name_or_path="deepset/roberta-base-squad2", use_gpu=True)
pipe = ExtractiveQAPipeline(reader, retriever)
#答案生成
prediction = pipe.run(query="Who is the father of Arya Stark?", top_k_retriever=10, top_k_reader=5)
graph LR
dicts -->document_store-->pipe-->prediction
注意上面提供的代码并不能直接运行,这里只是抽出核心的部分用于说明pipline的构造。从上面的流程图可以看出haystack的设计非常的清晰明了。
最简单的QA示例
下面直接提供源代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from haystack.document_store.elasticsearch import ElasticsearchDocumentStore
from haystack.reader.farm import FARMReader
from haystack.utils import print_answers
from haystack.retriever.sparse import ElasticsearchRetriever
# 注意:这里需要提前建好es服务
# 预料存储部件
document_store = ElasticsearchDocumentStore(host="localhost",port=9300, username="", password="", index="document")
docs=[{
'text':'''导数(Derivative),也叫导函数值。又名微商,是微积分中的重要基础概念。当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。
导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。
不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。然而,可导的函数一定连续;不连续的函数一定不可导。
对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。反之,已知导函数也可以反过来求原来的函数,即不定积分。
微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作,它们都是微积分学中最为基础的概念。'''
,'meta':{'name':'导数'}}]
document_store.write_documents(docs)
#检索部件
retriever = ElasticsearchRetriever(document_store=document_store)
#reader部件,相当于语义理解
reader = FARMReader(model_name_or_path="hfl/chinese-roberta-wwm-ext", use_gpu=True)
from haystack.pipeline import ExtractiveQAPipeline
#构造QA pipline
pipe = ExtractiveQAPipeline(reader, retriever)
#拿到答案
prediction = pipe.run(query="导数是什么", top_k_retriever=10, top_k_reader=5)
print_answers(prediction, details="minimal")
输出的答案为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
[ { 'answer': "增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。\n"
'导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该',
'context': "数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。\n"
'导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上'},
{ 'answer': "增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。\n"
'导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该',
'context': "数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f'(x0)或df(x0)/dx。\n"
'导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上'},
{ 'answer': '所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。\n'
'不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在',
'context': '是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。\n'
'不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则'},
{ 'answer': '所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。\n'
'不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在',
'context': '是实数的话,函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中,物体的位移对于时间的导数就是物体的瞬时速度。\n'
'不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在,则称其在这一点可导,否则'},
{ 'answer': '或其',
'context': '一定连续;不连续的函数一定不可导。\n'
"对于可导的函数f(x),x↦f'(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。反之,已知导函数也可以反过来求原来的函数,即不"}]
总结
本文走马观花式的介绍了haystack,然后实现了一个简单的QA。从下一篇文章起,我将首先介绍haystack的几个典型应用,在那之后详细的分析haystack的设计思路。